5-kW PM-SyRM

This example simulates sensorless current-vector control of a 5-kW permanent- magnet synchronous reluctance motor. Control look-up tables are also plotted.

import numpy as np

from motulator.drive import model
import motulator.drive.control.sm as control
from motulator.drive.utils import (
    BaseValues, NominalValues, plot, SynchronousMachinePars)

Compute base values based on the nominal values (just for figures).

nom = NominalValues(U=220, I=15.6, f=85, P=5.07e3, tau=19)
base = BaseValues.from_nominal(nom, n_p=2)

Configure the system model.

# Configure magnetically linear motor model
mdl_par = SynchronousMachinePars(
    n_p=2, R_s=.2, L_d=4e-3, L_q=17e-3, psi_f=.134)
machine = model.SynchronousMachine(mdl_par)
# Quadratic load torque profile
k = .05*nom.tau/(base.w/base.n_p)**2
mechanics = model.StiffMechanicalSystem(J=.0042, B_L=lambda w_M: k*np.abs(w_M))
converter = model.VoltageSourceConverter(u_dc=310)
mdl = model.Drive(converter, machine, mechanics)

Configure the control system.

par = mdl_par  # Assume accurate machine model parameter estimates
cfg = control.CurrentReferenceCfg(
    par, nom_w_m=base.w, max_i_s=2*base.i, k_u=.9)
ctrl = control.CurrentVectorControl(
    par, cfg, T_s=125e-6, J=.0042, sensorless=True)
ctrl.observer = control.Observer(
    control.ObserverCfg(par, sensorless=True, alpha_o=2*np.pi*200))
ctrl.speed_ctrl = control.SpeedController(
    J=.0042, alpha_s=2*np.pi*4, max_tau_M=1.5*nom.tau)

Plot control characteristics, computed using constant L_d, L_q, and psi_f.

# sphinx_gallery_thumbnail_number = 1
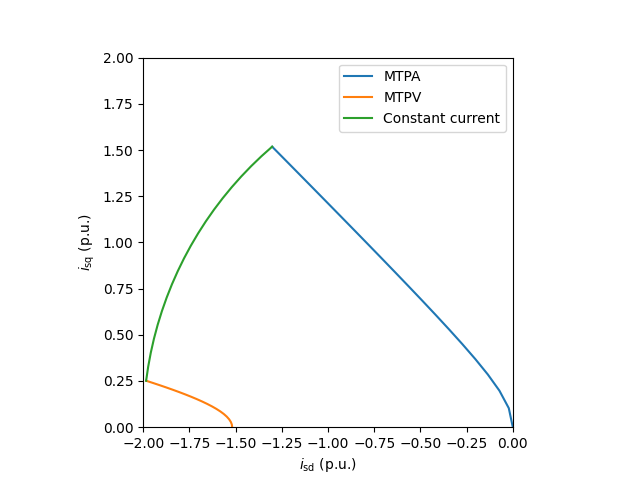
tq = control.TorqueCharacteristics(par)
tq.plot_current_loci(ctrl.current_reference.cfg.max_i_s, base)
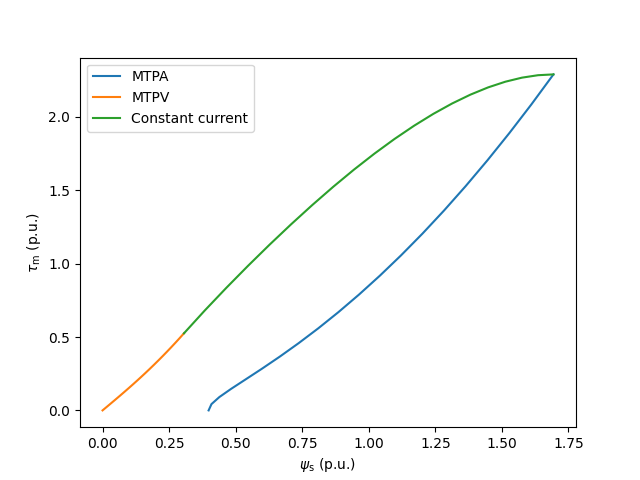
tq.plot_torque_flux(ctrl.current_reference.cfg.max_i_s, base)
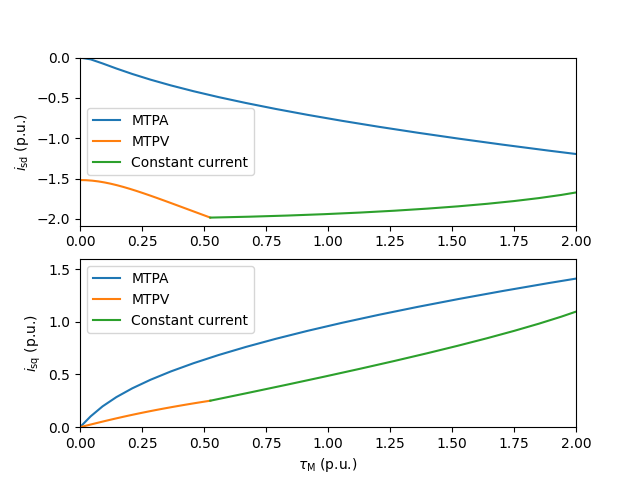
tq.plot_torque_current(ctrl.current_reference.cfg.max_i_s, base)
# tq.plot_flux_loci(ctrl.current_reference.cfg.max_i_s, base)

• 
• 
• 

Set the speed reference. The external load torque is zero (by default).

# Acceleration and load torque step
ctrl.ref.w_m = lambda t: (t > .1)*base.w*3

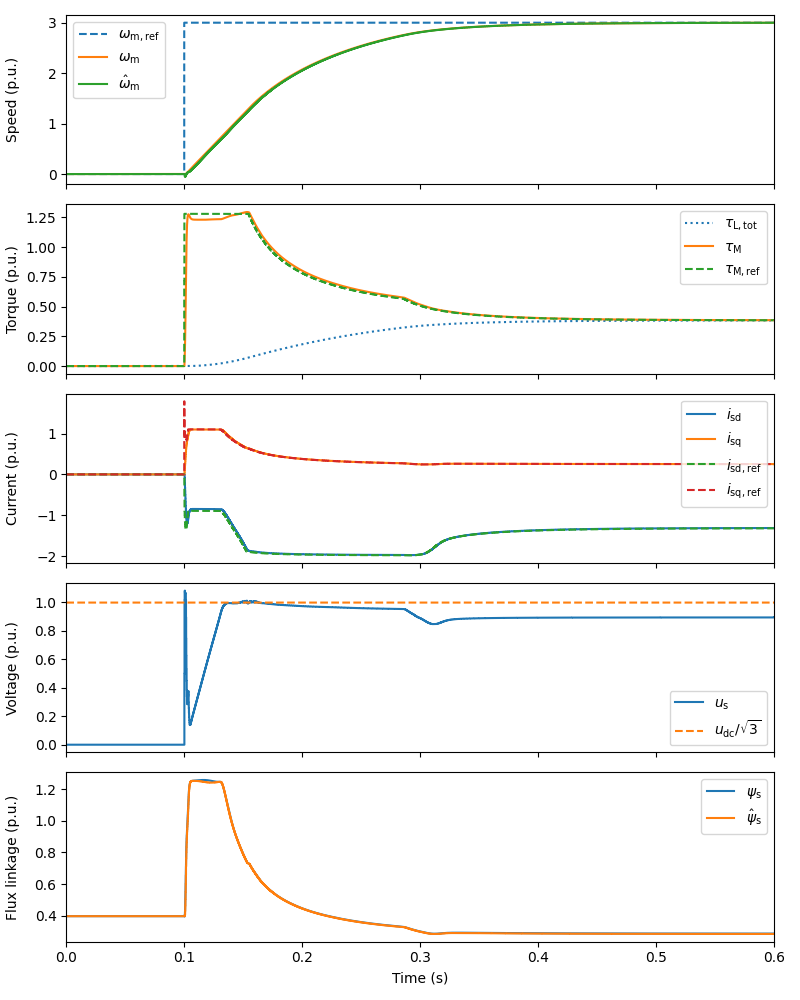
Create the simulation object, simulate, and plot results in per-unit values.

sim = model.Simulation(mdl, ctrl)
sim.simulate(t_stop=.6)
plot(sim, base)