12.5-kVA converter, disturbance observer

This example simulates a converter using disturbance-observer-based control in grid- forming mode. The converter output voltage and the active power are directly controlled, and grid synchronization is provided by the disturbance observer. A transparent current controller is included for current limitation.

from motulator.grid import control, model, utils

Compute base values based on the nominal values.

nom = utils.NominalValues(U=400, I=18, f=50, P=12.5e3)
base = utils.BaseValues.from_nominal(nom)

Configure the system model.

ac_filter = model.LFilter(L_f=0.15 * base.L, R_f=0.05 * base.Z, L_g=0.74 * base.L)
ac_source = model.ThreePhaseSource(w_g=base.w, e_g=base.u)
converter = model.VoltageSourceConverter(u_dc=650)
mdl = model.GridConverterSystem(converter, ac_filter, ac_source)

Configure the control system.

inner_ctrl = control.ObserverBasedGridFormingController(
    i_max=1.3 * base.i,
    L=0.35 * base.L,
    R=0.05 * base.Z,
    R_a=0.2 * base.Z,
    u_nom=base.u,
    w_nom=base.w,
)
ctrl = control.GridConverterControlSystem(inner_ctrl)

Set the references for converter output voltage magnitude and active power.

# Converter output voltage magnitude reference
ctrl.set_ac_voltage_ref(base.u)
ctrl.set_power_ref(
    lambda t: ((t > 0.2) / 3 + (t > 0.5) / 3 + (t > 0.8) / 3 - (t > 1.2)) * nom.P
)

# Uncomment line below to simulate operation in rectifier mode
# ctrl.ext_ref.p_g = lambda t: ((t > 0.2) - (t > 0.7) * 2 + (t > 1.2)) * nom.P

# Uncomment lines below to simulate a grid voltage sag with constant ref.p_g
# mdl.ac_filter.L_g = 0
# mdl.ac_source.e_g = lambda t: (1 - (t > 0.2) * 0.8 + (t > 1) * 0.8) * base.u
# ctrl.ext_ref.p_g = lambda t: nom.P

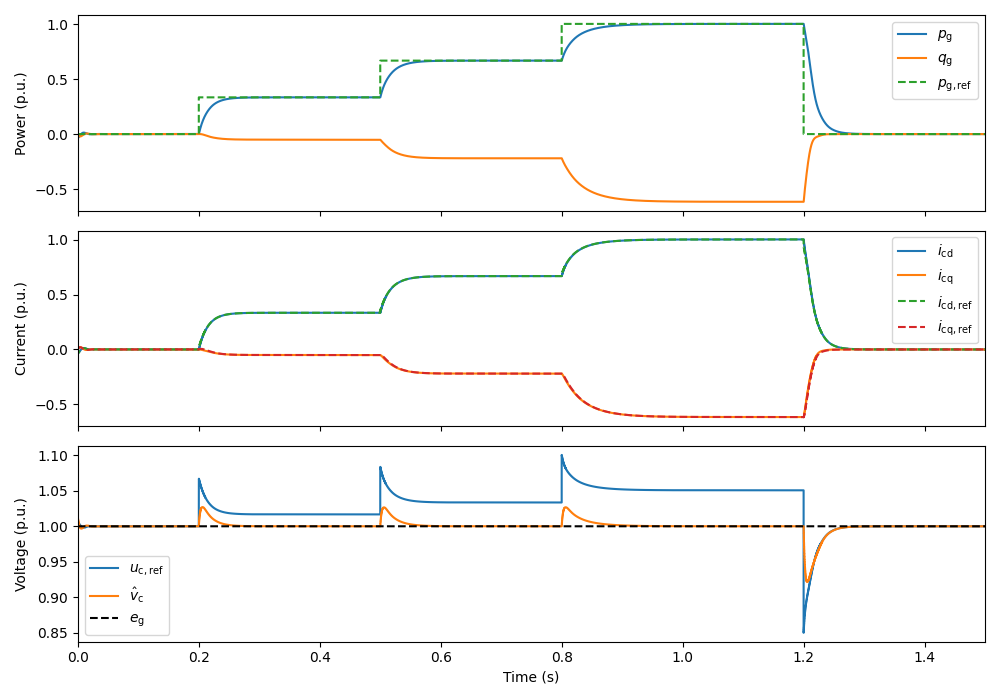
Create the simulation object, simulate, and plot the results in per-unit values.

sim = model.Simulation(mdl, ctrl)
res = sim.simulate(t_stop=1.4)
utils.plot(res, base)

• 
•