Note
Go to the end to download the full example code.
2.2-kW saturated IM, CVC#
This example simulates sensorless current-vector control (CVC) of a 2.2-kW induction motor (IM) drive. The magnetic saturation is included in the machine model, while the control system uses constant parameters.
from math import pi
import motulator.drive.control.im as control
from motulator.drive import model, utils
Compute base values based on the nominal values (just for figures).
nom = utils.NominalValues(U=400, I=5, f=50, P=2.2e3, tau=14.6)
base = utils.BaseValues.from_nominal(nom, n_p=2)
The main-flux saturation in the system model is modeled based on [1]. The default parameters correspond to the measured data of a 2.2-kW machine.
def L_s(psi: float, L_su: float = 0.34, beta: float = 0.84, S: float = 7) -> float:
"""Stator inductance saturation model."""
return L_su / (1 + (beta * psi) ** S)
Configure the system model.
# Γ-equivalent machine model with main-flux saturation included
par = model.InductionMachinePars(n_p=2, R_s=3.7, R_r=2.5, L_ell=0.023, L_s=L_s)
# Unsaturated machine model, using its inverse-Γ parameters (uncomment to try)
# par = model.InductionMachineInvGammaPars(
# n_p=2, R_s=3.7, R_R=2.1, L_sgm=0.021, L_M=0.224)
machine = model.InductionMachine(par)
mechanics = model.MechanicalSystem(J=0.015)
converter = model.VoltageSourceConverter(u_dc=540)
mdl = model.Drive(machine, mechanics, converter, pwm=False, delay=1)
Configure the control system.
# Machine model parameter estimates
est_par = control.InductionMachineInvGammaPars(
n_p=2, R_s=3.7, R_R=2.1, L_sgm=0.021, L_M=0.224
)
# est_par = par # Uncomment this line to use the perfectly known machine model
cfg = control.CurrentVectorControllerCfg(psi_s_nom=base.psi, i_s_max=1.5 * base.i)
vector_ctrl = control.CurrentVectorController(est_par, cfg, sensorless=True)
speed_ctrl = control.SpeedController(J=0.015, alpha_s=2 * pi * 4)
# speed_ctrl = control.PIController(k_p=1, k_i=1)
ctrl = control.VectorControlSystem(vector_ctrl, speed_ctrl)
Speed reference and the external load torque.
# Acceleration and load torque step
ctrl.set_speed_ref(lambda t: (t > 0.2) * 0.5 * base.w_M)
mdl.mechanics.set_external_load_torque(lambda t: (t > 0.75) * nom.tau)
# Field-weakening (uncomment to try)
# ctrl.set_speed_ref(lambda t: (t > 0.2) * 2 * base.w_M)
# mdl.mechanics.set_external_load_torque(lambda t: (t > 0.8) * 0.5 * nom.tau)
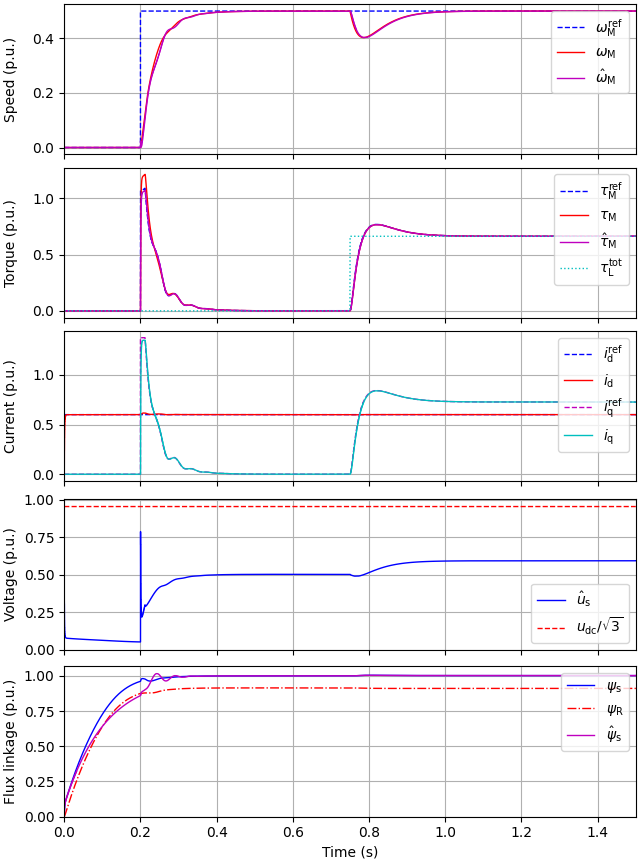
Create the simulation object, simulate, and plot the results in per-unit values.
sim = model.Simulation(mdl, ctrl)
res = sim.simulate(t_stop=1.5)
utils.plot(res, base) # Plot results in per-unit values
References
Total running time of the script: (0 minutes 5.268 seconds)