Note
Go to the end to download the full example code.
2.2-kW saturated IM, FVC#
This example simulates sensorless flux-vector control (FVC) of a 2.2-kW induction machine (IM) drive. The magnetic saturation is included in the machine model and taken into account in the control system. This example also applies the mechanical-model-based speed observer.
from math import pi
import motulator.drive.control.im as control
from motulator.drive import model, utils
Compute base values based on the nominal values (just for figures).
nom = utils.NominalValues(U=400, I=5, f=50, P=2.2e3, tau=14.6)
base = utils.BaseValues.from_nominal(nom, n_p=2)
Configure the system model. The Γ-equivalent machine model with main-flux saturation is used. The parameters are based on the measured data of a 2.2-kW machine [1].
par = model.InductionMachinePars(
n_p=2, R_s=3.7, R_r=2.5, L_ell=0.023, L_s=lambda psi: 0.34 / (1 + (0.84 * psi) ** 7)
)
machine = model.InductionMachine(par)
mechanics = model.MechanicalSystem(J=0.015)
converter = model.VoltageSourceConverter(u_dc=540)
mdl = model.Drive(machine, mechanics, converter)
Configure the control system.
est_par = par # Assume the machine model is perfectly known
# Since the inertia estimate `J` is provided below, the mechanical-model-based speed
# observer is used. You can disable the mechanical-model-based speed observer by
# removing the `J` parameter or setting it to `None`.
cfg = control.FluxVectorControllerCfg(
psi_s_nom=0.95 * base.psi,
i_s_max=1.5 * base.i,
J=0.015, # Inertia estimate enables the speed observer
alpha_i=0, # Integral action is not necessary with the speed observer
)
vector_ctrl = control.FluxVectorController(est_par, cfg, sensorless=True)
speed_ctrl = control.SpeedController(J=0.015, alpha_s=2 * pi * 4)
ctrl = control.VectorControlSystem(vector_ctrl, speed_ctrl)
Set the speed reference and the external load torque.
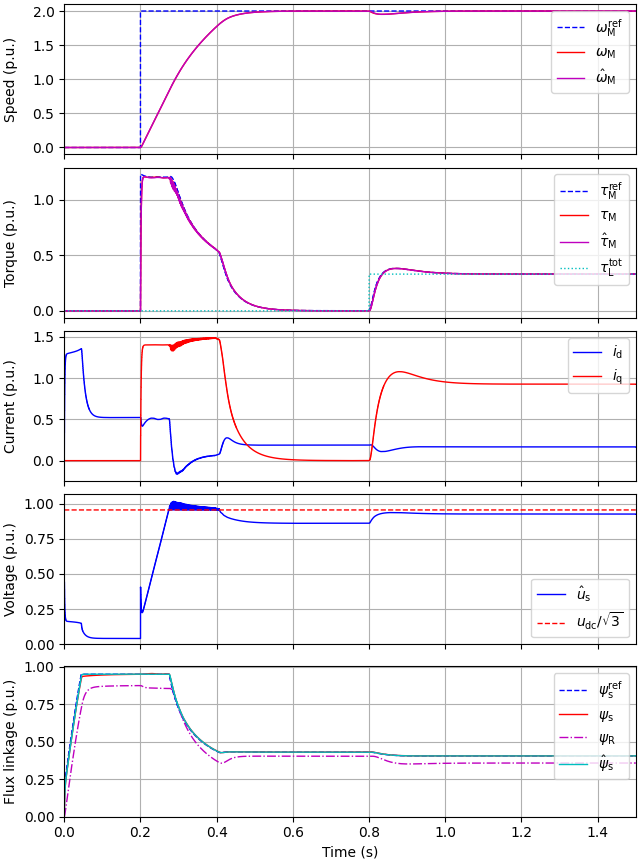
Create the simulation object, simulate, and plot the results in per-unit values.
sim = model.Simulation(mdl, ctrl)
res = sim.simulate(t_stop=1.5)
utils.plot(res, base)
References
Total running time of the script: (0 minutes 5.791 seconds)